快排及其优化

发表于 分类于 阅读次数：

快排的split实现和partition实现及其优化

快排的思想

快排的核心思想在于数组的划分，，通常我们将数组的第一个元素定义为比较元素，然后将数组中小于比较元素的数放到左边，将大于比较元素的放到右边，

这样我们就将数组拆分成了左右两部分：小于比较元素的数组；大于比较元素的数组。我们再对这两个数组进行同样的拆分，直到拆分到不能再拆分，数组就自然而然地以升序排列了。

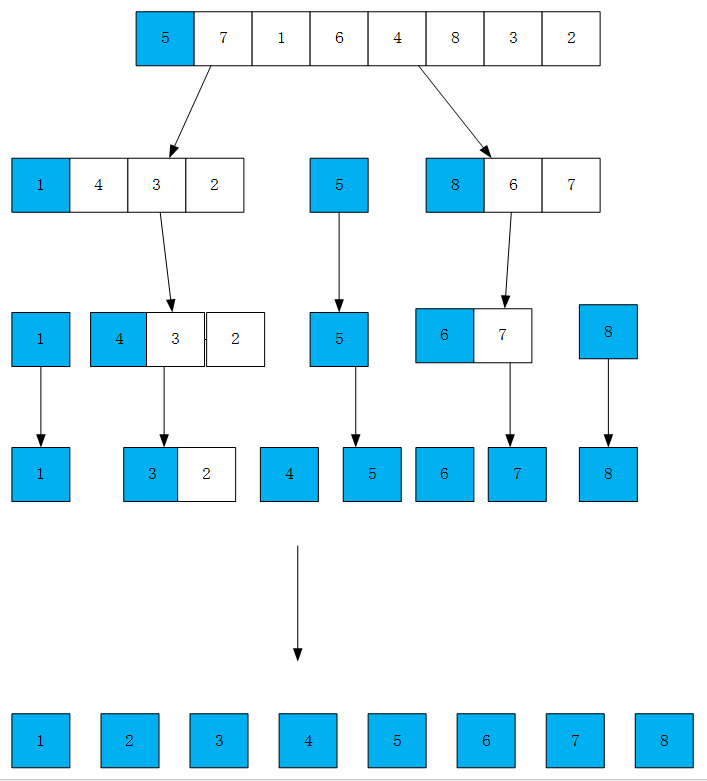
split算法

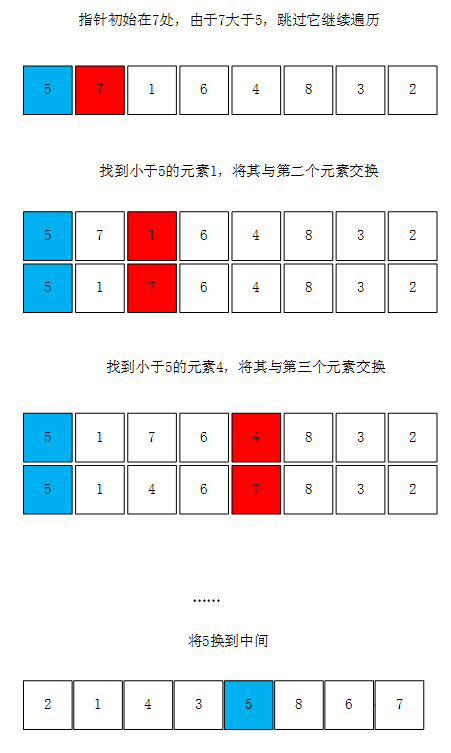
split算法使用一个单向的指针来对数组进行遍历，首先将数组首元素设置为比较元素，然后将第二个开始的元素依次与比较元素比较，如果大于比较元素则跳过，如果小于比较元素，则将其与前面较大的元素进行交换，将数组中所有元素交换完毕后，再将比较元素放到中间位置。简单来说就是让j在前面扫描所有的数，让i记录小于比较元素的值，j扫描到大于比较元素，就往前移动，然后等扫描到小于比较元素的位置就将其交换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//划分数组
    public static int split(int a[], int low, int high)
    {
        int i = low;    //i指向比较元素的期望位置
        int x = a[low];    //将该组的第一个元素作为比较元素
        //从第二个元素开始，若当前元素大于比较元素，将其跳过
        for(int j = low+1; j <= high; j++)
            //若找到了小于比较元素的元素，将其与前面较大的元素进行交换
            if(a[j] <= x)
            {
                i++;
                if(i != j)
                    swap(a, i, j);

            }
        swap(a, i, low);     //将比较元素交换到正确的位置上
        return i;    //返回比较元素的位置
    }

partition算法

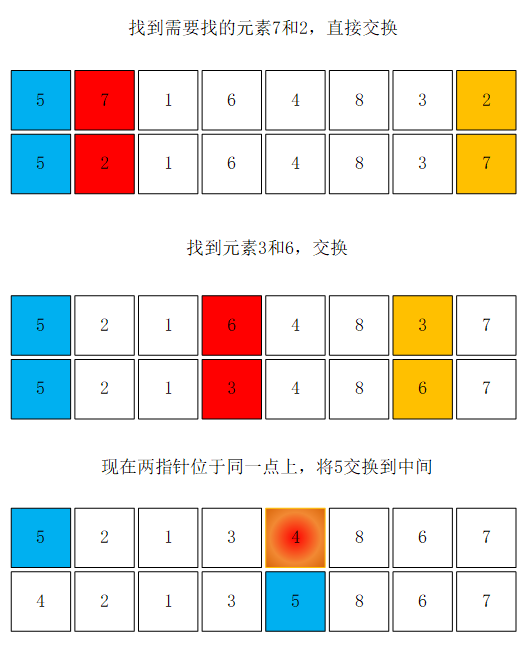
partition算法使用头尾两个方向相反的指针进行遍历，先将数组第一个元素设置为比较元素，头指针从左至右找到第一个大于比较元素的数，尾指针从右至左找到第一个小于比较元素的数，全部交换完毕后将比较元素放到中间位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//划分数组
    public static int partition(int a[], int low, int high)
    {
        int x = a[low];    //将该数组第一个元素设置为比较元素
        int i=low;
        int j=high;
        while(i < j)
        {
            while(i<j && a[i] <= x)
                i++;
            while(i<j && a[j] >= x)
                j--;


            if(i!=j)
                swap(a, i, j);
        }
        swap(a, j, low);
        return j;
    }

快排优化方法

当元素排列趋近有序或者有大量的相同元素，那么快排会退化成O(n2)的算法，可以从以下几个方面优化：

  • 三数取中法（Median-of-Three Partitioning）：选择子数组中的三个元素（通常是左端、中间和右端），取它们的中值作为枢纽元素。这样可以减少最坏情况发生的概率，提高排序的效率
  • 插入排序优化：在子数组较小（一般小于10个元素）时，采用插入排序而不是继续使用快速排序。插入排序在小数组上的效率较高，可以减少递归的层数，从而提高整体性能
  • 随机化：随机选择枢纽元素，以减少最坏情况发生的概率

三点中值法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//三点中值法
        public static int partition(int[] arr, int p, int r) {
            //优化，在p, r, mid之间，选一个中间值作为主元
            int midIndex = p + ((r - p) >> 1);//中间下标
            int midValueIndex = -1;//中值的下标
            if(arr[p] <= arr[midIndex] && arr[p] >= arr[r]) {
                midValueIndex = p;
            }else if(arr[r] <= arr[midIndex] && arr[r] >= arr[p]) {
                midValueIndex = r;
            }else {
                midValueIndex = midIndex;
            }
            swap(arr, p, midValueIndex);
            int pivot = arr[p];
            int left = p + 1; //左侧指针
            int right = r; //右侧指针
            while(left <= right) {
                while(left <= right && arr[left] <= pivot) {
                    left++;
                }
                while(left <= right && arr[right] > pivot) {
                    right--;
                }
                if(left < right) {
                    swap(arr, left, right);
                }
            }
            swap(arr, p, right);
            return right;
        }

三值中值和插入排序的实例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
import java.util.Arrays;
import java.util.Random;

public class OptimizedQuickSort {

    private static final int INSERTION_THRESHOLD = 10;

    public static void quickSort(int[] arr) {
        quickSort(arr, 0, arr.length - 1);
    }

    public static void quickSort(int[] arr, int left, int right) {
        if (right - left <= INSERTION_THRESHOLD) {
            insertionSort(arr, left, right);
        } else {
            int pivotIndex = medianOfThree(arr, left, right);
            int pivot = arr[pivotIndex];
            arr[pivotIndex] = arr[right];
            arr[right] = pivot;

            int i = left - 1;
            for (int j = left; j < right; j++) {
                if (arr[j] <= pivot) {
                    i++;
                    int temp = arr[i];
                    arr[i] = arr[j];
                    arr[j] = temp;
                }
            }
            int temp = arr[i + 1];
            arr[i + 1] = arr[right];
            arr[right] = temp;

            quickSort(arr, left, i);
            quickSort(arr, i + 2, right);
        }
    }

    private static int medianOfThree(int[] arr, int left, int right) {
        int mid = left + (right - left) / 2;
        if (arr[left] > arr[mid]) {
            swap(arr, left, mid);
        }
        if (arr[left] > arr[right]) {
            swap(arr, left, right);
        }
        if (arr[mid] > arr[right]) {
            swap(arr, mid, right);
        }
        return mid;
    }

    private static void insertionSort(int[] arr, int left, int right) {
        for (int i = left + 1; i <= right; i++) {
            int key = arr[i];
            int j = i - 1;
            while (j >= left && arr[j] > key) {
                arr[j + 1] = arr[j];
                j--;
            }
            arr[j + 1] = key;
        }
    }

    private static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    public static void main(String[] args) {
        int[] arr = {38, 27, 43, 3, 9, 82, 10};
        quickSort(arr);
        System.out.println(Arrays.toString(arr)); // Output: [3, 9, 10, 27, 38, 43, 82]
    }
}