二分查找-红蓝染色法总结
二分查找-红蓝染色法
L, R分别指向数组的左右边界及闭区间[L,R],红色背景表示不满足条件,蓝色表示满足条件,白色表示不确定
开闭区间问题
闭区间(常用):[0, nums.length - 1] 退出二分查找需要left <= right, 移动区间时 left = mid + 1, right = mid - 1,这样才不会出现死循环。
左闭右开:[0, nums.length) 退出二分查找需要left < right, 移动区间时 left = mid + 1, right = mid
开区间:(-1, nums.length) 退出二分查找需要left+1 < right, 移动区间时 left = mid, right = mid
思想:使用二分查找去查找target的第一个位置,如果第一个满足位置是数组长度说明整个数组都是红色,或者返回的值不等于target,不符合条件。再使用二分查找去找target+1的前一个位置。
二分查找(红蓝染色)的思想:利用数组有序的性质,从左右两端开始快速查找符合的target范围,如果nums[mid]小于target,left=mid+1,从右侧开始查找,反之亦然,找到符合条件的第一个target位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public int[] searchRange(int[] nums, int target) {
int start = lowerBound(nums, target);
if(start == nums.length || nums[start] != target) {
return new int[]{-1, -1};
}
int end = lowerBound(nums, target+1);
return new int[]{start, end -1};
}
private int lowerBound(int[] nums, int target) {
int left = 0, right = nums.length-1;
int mid = 0;
while(left <= right) {
mid = left + (right - left) / 2;
if(nums[mid] < target) {
left = mid+1;
}else {
right = mid - 1;
}
}
return left;
}
}
|
非>= k 问题如何转化(在有序数组问题中)
“>k”可以看作是>= k+1
“<k”可以看作 (>=k) -1,即找到大于等于k的位置的前一个位置
“<=k”可以看作(>k) -1,即找到大于k的位置的前一个位置
蓝色是峰值及其右侧,right = nums.length - 1, nums[right]一定是蓝色,预留这个位置
每次二分确定一半的颜色
简单来说就是当有nums[mid] > nums[mid + 1]就能确定是一个下坡,至少有一个峰值,如果nums[mid]之前是上坡,那么nums[mid]就是峰值,nums[mid]之前是下坡,也能确定一个峰值
1
2
3
4
5
6
7
8
9
10
11
| class Solution {
public int findPeakElement(int[] nums) {
int left = -1, right = nums.length - 1;
while (left + 1 < right) {
int mid = left + (right - left) / 2;
if (nums[mid] > nums[mid + 1]) right = mid;
else left = mid;
}
return right;
}
}
|
red:最小值左侧
blue:最小值及其右侧
5 6 7 8 2 3 4
num[right]一定是蓝色,大于等于num[right]肯定要舍弃染成红色,最小值肯定小于num[right],选择左侧区域寻找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public int findMin(int[] nums) {
int left = -1, right = nums.length - 1;
while(left+1 < right) {
int mid = left + (right - left) / 2;
if(nums[mid] < nums[right]){
right = mid;
}else {
left = mid;
}
}
return nums[right];
}
}
|
本题与 153 的区别在于有相同元素,这会导致在二分查找时,可能会遇到「恰好」二分元素与数组末尾元素相同的情况,此时无法确定答案在左半区间还是右半区间。
我们接着 153 题解 的代码来实现。本题需要稍加修改,改为与区间右端点处的元素比较(如果你写的是闭区间的话,那就是与右端点 +1 的元素比较)。
在遇到相同元素时,既然无法确定最小值所在区间,那么干脆去掉末尾元素,继续二分。对应到代码上,就是 right 减一
你可能会有疑问:这样做不会碰巧把最小值给去掉吗?这是不会的:
- 如果末尾元素就是最小值,那么nums[mid] 也是最小值,说明最小值仍然在二分区间中;
- 如果末尾元素不是最小值,这样做相当于排除了一个错误答案。
1
2
3
4
5
6
7
8
9
10
11
12
| class Solution {
public int findMin(int[] nums) {
int left = -1, right = nums.length - 1;
while (left + 1 < right) {
int mid = (left + right) >>> 1;
if (nums[mid] < nums[right]) right = mid;
else if (nums[mid] > nums[right]) left = mid;
else --right;
}
return nums[right];
}
}
|
red:目标target左侧
blue:目标target及其右侧
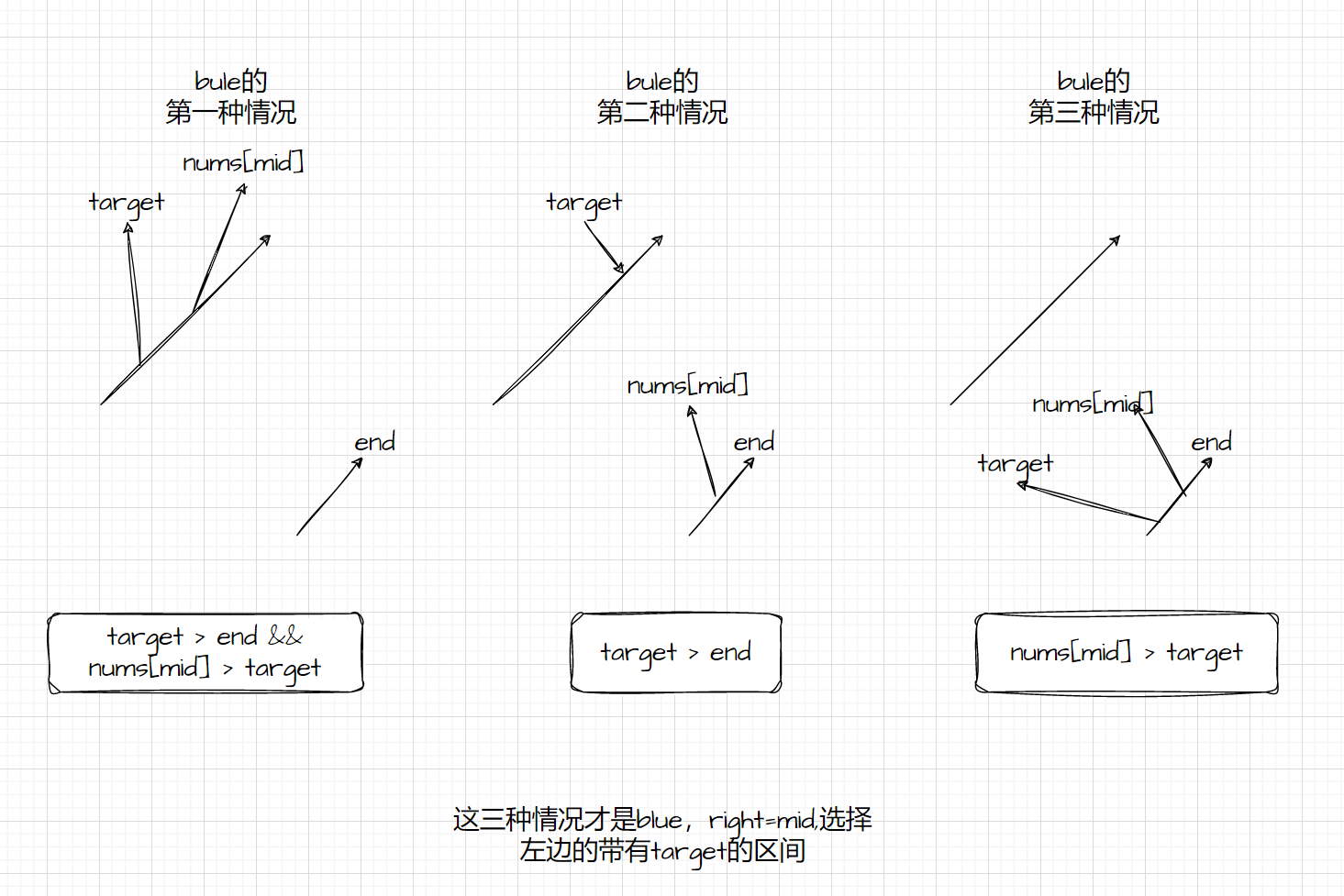
当nums[mid]>end时,在左侧:
- nums[mid ] > target 可以缩小蓝色区间, right=mid
当nums[mid]<end时,在右侧:
- 当nums[mid]已经在右侧,target>end说明target还在左侧,即可缩小蓝色区间
- 当nums[mid] > target,与第一种情况同理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public int search(int[] nums, int target) {
int left = -1, right = nums.length - 1;
while (left + 1 < right) {
int mid = left + (right - left) / 2;
if (isBlue(nums, target, mid)) right = mid;
else left = mid;
}
return nums[right] == target ? right : -1;
}
private boolean isBlue(int[] nums, int target, int mid) {
int end = nums[nums.length - 1];
if (nums[mid] > end) {
return target > end && nums[i] >= target;
}
return target > end || nums[i] >= target;
}
}
|
